This section deals with the data-storage elements of Fortran: constants, variables, and arrays. These all possess an important property called data type. The data type of an item determines what sort of information it holds and the operations that can be performed on it.
All the information processed by a digital computer is held internally in the form of binary digits or bits. Suitable collections of bits can be used to represent many different types of data including numbers and strings of characters. It is not necessary to know how the information is represented internally in order to write Fortran programs, only that there is a different representation for each type of data. The data type of each item also determines what operations can be carried out on it: thus arithmetic operations can be carried out on numbers, whereas character strings can be split up or joined together. The data type of each item is fixed when the program is written.
Fortran, with its emphasis on numerical operations, has four data types just for numbers. These are collectively known as the arithmetic data types. Arithmetic expressions can include mixtures of data types and, in most cases, automatic type conversions are provided. In other circumstances, however, especially in procedure calls, there is no provision for automatic type conversion and it is essential for data types to match exactly.
The range and precision of the arithmetic data types are not specified by the Standard: typical values are indicated below, but the only way to be sure is to check the manuals provided with your own Fortran system.
Several intrinsic functions are available to convert from one data type to another. Conversion from character strings to numbers and vice-versa can be complicated; these are best carried out with the internal file READ and WRITE statements (see section 10.3).
There are, as yet, no user-defined or structured data types in Fortran.
The table below summarises the properties of the six data types provided in Standard Fortran:
The first four types (integer, real, double precision, and complex) all hold numerical information and are collectively known as arithmetic data types.
The integer data type can only represent whole numbers but they are stored exactly in all circumstances. Integers are often used to count discrete objects such as elements of an array, characters in a string, or iterations of a loop.
The range of numbers covered by the integer type is system-dependent. The majority of computers use 32 bits for their integer arithmetic (1 bit for the sign and 31 for the magnitude) giving a number range of -2,147,483,648 to +2,147,483,647. Some systems have an even larger integer range but a few very small systems only allow 16-bit integer arithmetic so that their integer range is only -32,768 to +32,767.
Most scientific applications use the real data type more than anything else. Real values are stored internally using a floating-point representation which gives a larger range than the integer type but the values are not, in general, stored exactly. Both the range and precision are machine dependent.
In practice most machines use at least 32 bits to store real numbers.
Many systems now use the IEEE Standard representation: for 32-bit
numbers this gives a precision of just over 7 decimal digits and allows a
number range from around 
to just over 
. This can be
something of a limitation because there are many types of calculation,
especially in physics and astronomy, which lead to numbers in excess of
. Some computers designed expressly for scientific work,
sometimes called ``super-computers", allocate 64 bits for real numbers so
that the numerical precision is much larger; the range is often larger as
well. On such machines it is rarely necessary to use the double
precision type.
Double precision is an alternative floating-point type. The Fortran Standard only specifies that it should have greater precision than the real type but in practice, since the double precision storage unit is twice the size, it is safe to assume that the precision is at least doubled. The number range may, however, be the same as that for real type.
Although double precision values occupy twice as much memory as real (or integer) values, computations on them do not necessarily take twice as long.
The complex data type stores two real values as a single entity. There is no double precision complex type in Standard Fortran.
Complex numbers arise naturally when extracting the roots of
negative numbers and are used in many branches of mathematics,
physics, and engineering. A complex number is often represented
as (A + iB), where A and B are the real and imaginary parts
respectively and 
. Electrical engineers, having used the
letter i to represent current, use the notation (A + jB) instead.
Although the rules for manipulating complex numbers are straight-forward, it is convenient to have the Fortran system to do the work. It is usually more efficient as well, because the computer can use its internal registers to store the intermediate products in complex arithmetic. Exponentiation and the four regular arithmetic operators can be used on complex values, and various intrinsic functions are also provided such as square-root, logarithms, and the trigonometric functions.
The logical data type is mainly used in conjunction with IF statements which select a course of action according to whether some condition is true or false. A logical variable (or array element) may be used to store such a condition value for future use. Logical variables and arrays are also useful when dealing with two-valued data such as whether a person is male or female, a file open or closed, power on or off, etc.
Some programmers seem reluctant to use logical variables and arrays because they feel that it must be inefficient to use an entire computer word of perhaps 32 bits to store just one bit of information. In fact the extra code needed to implement a more efficient data packing scheme usually wastes more memory than the logical variables would have occupied.
The character type is unique in that each character item has a length defined for it: this is the number of characters that it holds. In general the length is fixed when the item is declared and cannot be altered during execution. The only exception to this is for dummy arguments of procedures: here it is possible for the dummy argument to acquire the length of the corresponding actual argument. Using this facility, general-purpose procedures can be written to operate on character strings irrespective of their length. In addition, the rules for character assignment take care of mismatched lengths by truncating or padding with blanks on the right as necessary. This means that the Fortran character type has many of the properties of a genuine variable-length character-handling system.
The maximum length of a character item is system-dependent: it is safe to assume that all systems will allow strings of up to 255 characters, a length limit of 32767 (or even more) is quite common. The minimum length of a character item is one character; empty or null strings are not permitted.
Although the Fortran Standard does not specify the absolute amount of memory to be allocated to each data type, it does specify the relative amounts. This is not important very often, only when constructing unformatted direct-access records or when using COMMON and EQUIVALENCE statements. The rules are as follows:
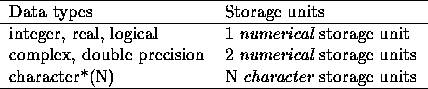
In the case of an array the number of storage units must be multiplied by the total number of elements in the array.
The relationship between the numeric and character storage units is deliberately undefined because it is entirely system-dependent.
It is usually fairly clear which data type to choose for each item in a program, though there are some borderline cases among the various arithmetic data types.
When processing data which are inherently integers, such as the number of seeds which germinate in each plot, or the number of photons detected in each time interval, it is not always clear whether to use integer or real arrays to store them. They both use the same memory space but on some machines additions and subtractions are faster on integers than on floating-point numbers. In practice, however, any savings can be swallowed up in the data type conversions that are usually necessary in subsequent processing. The main snag with integers is the limited range; on some machines integer overflow is not detected whereas floating-point overflows nearly always produce error messages.
If your machine stores its real variables in 32-bit words then the
precision of around 1 in 
is likely to be inadequate in some
applications. This imprecision is equivalent to an error of several
pence in a million pounds, or around ten milliseconds in a day. If
errors of this order are significant you should consider using the
double precision type instead. This will normally reduce the errors
by at least another factor of . Mixing data types increases the
risks of making mistakes and it is often simpler and safer to use the
double precision type instead of real throughout the program, even
though this may use slightly more memory and processor time.
Although automatic type conversions are provided for the arithmetic types in expressions, in other cases such as procedure calls it is essential for each actual argument to have the same data type as the corresponding dummy argument. Since program units are compiled independently, it is difficult for either the compiler or the linker to detect type mismatches in calls to external procedures.
Although Standard Fortran only provides the above six data types, many systems provide additional ones. You may come across data type names such as: LOGICAL*1, INTEGER*2, REAL*8, COMPLEX*16, etc. The number after the asterisk indicates the number of bytes of storage used for each datum (a byte being a group of 8 bits). This notation has a certain logic but is totally non-standard. The use of a term like REAL*8 when it is simply a synonym for DOUBLE PRECISION seems particularly pointless. There are, of course, circumstances when types such as COMPLEX*16 are necessary but the price to be paid is the loss of portability.
A constant has a value which is fixed when the program is written. The data type of every constant is evident from its form. Arithmetic constants always use the decimal number base: Standard Fortran does not support other number bases such as octal or hexadecimal.
Although arithmetic constants may in general have a leading sign (plus or minus) there are some circumstances in Fortran when an unsigned constant is required. If the constant is zero then any sign is ignored.
The general form of an integer constant is a sign (plus or minus)
followed by a string of one or more digits. All other characters
(except blanks) are prohibited. If the number is positive the plus
sign is optional. Here are some examples of valid integer
constants:
-100 42 0 +1048576
It is easier to read a large number if its digits are marked off in
groups of three: traditionally the comma (or in some countries the
dot) is used for this purpose. The blank can be used in the same
way in Fortran programs (but not in data files):
-1 000 000 000
Note that this number, although conforming to the rules of Fortran,
may be too large in magnitude to be stored as an integer on some
systems.
A real constant must contain a decimal point or an exponent (or
both) to distinguish it from one of integer type. The letter ``E" is
used in Fortran to represent ``times 10 to the power of". For
example, the constant 
is written as ``1.234E-5".
The most general form of a real constant is:
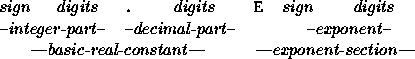
Both signs are optional; a plus sign is assumed if no sign is
present. Leading zeros in the integer-part and in the exponent are
ignored. Either the integer part or the decimal part may be omitted
if it is zero but one or the other must be present. If the value of the
exponent is zero the entire exponent section may be omitted
provided a decimal point is present in the number.
There is no harm in giving more decimal digits in a real (or double precision) constant than the computer can make use of: the value will be correctly rounded by the computer and the extra decimal places ignored.
Here are a few examples of valid real constants:
.5 -10. 1E3 +123.456E4 .000001
Dangling decimal points, though permitted, are easily overlooked,
and it is conventional to standardize constants in exponential
notation so that there is only one digit before the decimal point.
Using this convention, these values would look like this:
0.5 -10.0 1000.0 1.23456E6 1.0E-6
A double precision constant has a similar form to a real constant
but it must contain an exponent but using the letter ``D" in place of
"E" even if the exponent is zero. Some examples of double
precision constants are:
3.14159265358987D0 1.0D-12 -3.652564D+02
A complex constant has the form of two real or integer constants
separated by a comma and enclosed in a pair of parentheses. The
first number is the real component and the second the imaginary
component. Some examples of valid complex constants are:
(3.14,-5.67) (+1E5,0.125) (0,0) (-0.999,2.718E15)
There are only two possible logical constants, and they are expressed as: .TRUE. and .FALSE. The dots at each end are needed to distinguish these special forms from the words TRUE and FALSE, which could be used as symbolic names.
A character constant consists of a string of characters enclosed in a pair of apostrophes which act as quotation marks. Within the quoted string any characters available in the character set of the machine are permitted; the blank (or space) character is significant within character constants and counts as a single character just like any other. Examples of valid character constants are:
'X'
' œ40 + 15%'
'This is a constant including spaces'
The apostrophe character can be included in a character constant
by representing it as two successive apostrophes (with no
intervening blanks). This pair of apostrophes only counts as a
single character for the purposes of computing the length of the
string. For example: 'DON''T' is a constant of length 5.
The preceding rules ensure that the data type of an literal constant is completely determined by its form. Similarly the data type of an expression depends on the operands and operators involved. The intrinsic functions are also a special case, since their properties, including their data types, are known to the compiler. All other typed objects in a Fortran program are referred to by symbolic names. The rules given here apply to all of these named objects: variables, arrays, named constants, statement functions, and external functions.
In many programming languages, especially those in the Algol family, the data type of almost every item in the program has to be specified explicitly. Many programmers regard it as a chore to have to provide all these type specifications, although their presence does make it rather easier for the compiler to detect mistakes.
In Fortran you can specify data types explicitly in a similar way by using type statements, but Fortran also makes life easier by having certain default types. The data type of any object which has not been declared in a type statement depends on the first letter of its name. The default rules are:
Most programs make extensive use of integer and real objects, so these default values reduce the number of type statements that are required, provided suitable initial letters are chosen for the symbolic names.
The first-letter rule can also be changed throughout a program unit by using an IMPLICIT statement, described below.
There are six different type statements, one for each data type. In their simplest form they just consist of the appropriate data-type keyword followed by a list of symbolic names. For example:
INTEGER AGE, GRADE
LOGICAL SUPER
REAL RATE, HOURS, PAY, TAX, INSURE
In this example the first four items declared to be real would have had that type anyway had the default rules been left to operate. Confirmatory type specification does no harm.
There is no limit to the number of type statements that can be used but a name must not have its type specified explicitly more than once in a program unit. Type statements must precede all executable statements in the unit; it is good practice, though not essential, for them to precede other specification statements referring to the same name. Type statements can be used in a subprogram to specify the types of the dummy arguments and, in an external function, the type of the function as well. Type statements by themselves have no effect on intrinsic function names but it is not a good idea to use them in this way.
The CHARACTER statement is slightly different from the others
because it also specifies the length of each character item, i.e. the
number of characters it holds. The length can be given separately
for each item, thus:
CHARACTER NAME*15, STREET*30, TOWN*20, PCODE*7
Alternatively, if several items are to have the same length, a default
length for the statement can be given at the beginning:
CHARACTER*20 STAR, GALAXY, COMET*4, PLANET
This declares the name COMET to have a length of 4 characters,
whereas STAR, GALAXY, and PLANET are all 20 characters
long. If the length is not specified at all it defaults to one. The
length can also be specified by means of a named integer constant
or an integer constant expression enclosed in parentheses. For
example:
PARAMETER (NEXT=15, LAST=80)
CHARACTER TEXT*(NEXT+LAST)
Note that the length of a character item is fixed at compilation
time. The special form:
CHARACTER NAME*(*)
is permitted in two cases: for named constants the length of the
literal constant in the PARAMETER statement is used (section
5.4); for dummy arguments of procedures the length of the
associated actual argument is used (section 9.5). Type statements
can also be used to declare the dimensions of arrays: this is
described in section 5.6.
The IMPLICIT statement can be used to change the first-letter
default rule throughout a program unit. For example:
IMPLICIT DOUBLE PRECISION (D,X-Z), INTEGER (N-P)
would mean that all names starting with the letters D,X,Y, or Z
would (unless declared otherwise in type statements) have the type
double precision. Similarly the letters I through P, instead of just
I through N, will imply integer type. The other letters (A-C,E-H,
and Q-W) will still imply real type.
IMPLICIT can be used with character type to specify a default
length as well, for example:
IMPLICIT CHARACTER*100 (C,Z), CHARACTER*4 (S)
But this is not usually of much practical value. As with type
statements, the default character length is one.
More than one IMPLICIT statement can be used in a program unit but the same letter must not have its implied type specified more than once. The usual Fortran implied-type rules apply to all initial letters not listed in any IMPLICIT statements. The list of letters given after each type must appear in alphabetical order. IMPLICIT statements normally precede all other specification statements in a program. There is one exception to this: PARAMETER statements may precede them provided that the constants named in them are not affected by the IMPLICIT statement. Note that dummy arguments and function names may be affected by a subsequent IMPLICIT statement. IMPLICIT statements have no effect on intrinsic function names.
There are two diametrically opposed schools of thought on type
specification. The first holds that all names should have their
types specified explicitly. This certainly helps programmers to
avoid mistakes, because they have to think more carefully about
each item. It also helps the compiler to diagnose errors more
easily, especially if the it knows that all names are going to be
declared in advance. Some Fortran compilers allow a statement of
the form ``IMPLICIT NONE" which makes all names typeless by
default and so requiring every name to be explicitly typed. Others
have a compile-time switch with the same effect. If yours does not
you may be able to produce a similar effect by using something
like:
IMPLICIT CHARACTER*1000000 (A-Z)
near the beginning of each program unit which is likely to cause an
error for anything not explicitly typed. One disadvantage of the
practice of declaring all names in advance is that the program may
become so cluttered with specification statements that it may
obscure its structure and algorithm.
The alternative way of working is to make maximum use of implicit types to reduce the number of statements. This means, of course, that the first letter of each name has to be chosen to suit the type, leaving no more than five to be chosen freely: this makes it harder than ever to devise meaningful symbolic names. As a result, Fortran programs often include names like RIMAGE or ISIZE or KOUNT. Clearly type statements are still needed for character type because it is usually necessary to use items of a number of different lengths.
Experience suggests that either system can be satisfactory provided it is used consistently. However the wholesale reassignment of initial letters with IMPLICIT statements usually increases the chance of making a mistake. IMPLICIT, if used at all, should only reassign one or two rarely-used letters to the less common data types, for example:
IMPLICIT DOUBLE PRECISION (Z), LOGICAL (Q),
COMPLEX (X)
It is also prudent to use an identical IMPLICIT statement in each
program unit, otherwise type mismatches are more likely to be
made in procedure calls.
The PARAMETER statement can be used to give a symbolic name to any constant. This can be useful in several rather different circumstances.
With constants of nature (such as 
) and physical conversion
factors (like the number of pounds in a kilogram) it can save typing
effort and reduce the risk of error if the actual number is only
given once in the program and the name used everywhere else:
REAL PI, TWOPI, HALFPI, RTOD
PARAMETER (PI = 3.14159265, TWOPI = 2.0 * PI)
PARAMETER (HALFPI = PI / 2.0, RTOD = 180.0 / PI)
The names PI, TWOPI, etc. can then be used in place of the
literal
constants elsewhere in the program unit. It is much better to use
named constants than variables in such cases as they are given
better protection against inadvertent corruption: constants are often
protected by hardware. The use of symbolic names rather than
numbers can also make the program a little more readable: it is
probably harder to work out the significance of a number like
1.570796325 than to deduce the meaning of HALFPI.
Another important application of named constants is for items which are not permanent constants but parameters of a program, i.e. items fixed for the present but subject to alteration at some later date. Named constants are often used to specify array bounds, character-string lengths, and so on. For example:
INTEGER MAXR, MAXC, NPTS
PARAMETER (MAXR = 100, MAXC = 500, NPTS = MAXR*MAXC)
REAL MATRIX(MAXR,MAXC), COLUMN(MAXR), ROW(MAXC)
The constants such as MAXR and MAXC can also be used in the
executable part of the program, for instance to check that the array
subscripts are in range:
IF(NCOL .GT. MAXC .OR. NROW .GT. MAXR) THEN
STOP 'Matrix is too small'
ELSE
MATRIX(NROW,NCOL) = ROW(NCOL)
END IF
If, at some point, the matrix turns out to be too small for your
needs then you only have to alter this one PARAMETER
statement: everything else will change automatically when the
program is recompiled.
The rules for character assignment apply to PARAMETER statements: see section 7.4. In addition a special length specification of *(*) is permitted which means that the length of item is set to that of the literal constant. The type specification must precede the PARAMETER statement.
CHARACTER*(*) LETTER, DIGIT, ALPNUM
PARAMETER (LETTER = 'ABCDEFGHIJKLMNOPQRSTUVWXYZ',
$ DIGIT = '0123456789', ALPNUM = LETTER // DIGIT)
CHARACTER WARN*(*)
PARAMETER (WARN = 'This matrix is nearly singular')
The constant ALPNUM will be 36 characters long and contain all
the alpha-numeric characters (letters and digits).
Named logical constants also exist, but useful applications for them are somewhat harder to find:
PARAMETER (NX = 100, NY = 200, NZ = 300, NTOT = NX*NY*NZ)
LOGICAL LARGE
PARAMETER (LARGE = (NTOT .GT. 1000000) .OR. (NZ .GT. 1000))
The general form of the PARAMETER statement is:
PARAMETER ( cname = cexp, cname = cexp, ... )
where each cname is a symbolic name which becomes the name of
a constant, and each cexp is a constant expression of a suitable
data type.
The terms in a constant expression can only be literal constants or named constants defined earlier in the same program unit. Variables, array elements, and function references are not permitted at all. Otherwise the usual rules for expressions apply: parentheses can be used around sub-expressions, and the arithmetic types can be intermixed. There is one restriction on exponentiation: it can only be used to raise a number to an integer power. The normal rules for assignment statements apply: for arithmetic types suitable conversions will be applied if necessary; character strings will be truncated or padded to the required length. Note that substring references are not permitted in character constant expressions.
PARAMETER statements are specification statements and may precede or follow type statements. But any type (or IMPLICIT) statement which affects the data type or length of a named constant must precede it. Subject to these rules, PARAMETER statements are permitted to precede IMPLICIT statements. This makes it possible for a named constant to set the default length for the character type for certain ranges of initial letters. For example:
PROGRAM CLEVER
PARAMETER (LENCD = 40, LENE = 2 * LENCD)
IMPLICIT CHARACTER*(LENCD)(C-D), CHARACTER*(LENE)(E)
PARAMETER (DEMO = 'This is exactly 40 chars long')
Once defined, a named constant can be used in any expression,
including a dimension-bound expression, or in a DATA statement.
A named constant cannot be used just as part of another constant
(for example one component of a complex constant) and named
constants are not permitted at all within format specifications.
One of the limitations of Standard Fortran at present is that there is no way of allocating memory dynamically. One of the best ways around this is to use named constants to specify array bounds; this makes it much easier to alter programs to suit new requirements.
Names should also be given to all mathematical and physical constants that your programs require. If the same constants are needed in several program units then it may be sensible to compose a suitable set of PARAMETER statements for all of them and bring them in where ever necessary using INCLUDE statements.
If you define double precision constants in a PARAMETER statement do not forget that each literal constant value must include an exponent using the letter D.
There are no constant arrays in Fortran: the only way to overcome this limitation is to declare an ordinary array in a type statement and initialise its elements with a DATA statement (described in section 11).
A variable is simply a named memory location with a fixed data type. As explained earlier, variables do not have to be declared in advance if the data type implied by the first letter of the name is appropriate. Otherwise a type statement is required.
At the start of execution the value of each variable is undefined unless a suitable DATA statement appears in the program unit (see section 11). Undefined values must not be used in expressions. Local variables in procedures do not necessarily retain their values from one invocation of the procedure to another unless a suitable SAVE statement is provided (section 9.11).
An array is a group of memory locations given a single name. The elements of the array all have the same data type.
In mathematics the elements of an array a would be denoted by a1, a2, a3, and so on. In Fortran a particular array element is identified by providing a subscript expression in parentheses after the array name: A(1), A(2), A(3), etc. Subscripts must have integer type but they may be specified by expressions of arbitrary complexity, including function calls.
An array element can be used in the same way as a variable in almost all executable statements. Array elements are most often used within loops: typically an integer loop counter selects each element of the array in turn.
*Add array OLD to array NEW making array TOTAL
PARAMETER (NDATA = 1024)
REAL OLD(NDATA), NEW(NDATA), TOTAL(NDATA)
*......
DO 100, I = 1,NDATA
TOTAL(I) = OLD(I) + NEW(I)
100 CONTINUE
Arrays can have up to seven dimensions; the lower bound of each dimension is one unless declared otherwise. There is no limit on the upper bound provided it is not less than the lower bound. Arrays which are dummy arguments of a procedure may have their dimension bounds specified by integer variables which are arguments of the procedure; in all other cases each dimension bound must be an integer constant expression. This fixes the size of the array at compile-time.
Type, DIMENSION, and COMMON statements may all be used
to declare arrays, but COMMON statements have a specialised use
(described in section 12). The DIMENSION statement has a
similar form to a type statement but only declares the bounds of an
array without determining its data type. It is usually simpler and
neater to use a type statement which specifies both at once:
CHARACTER COLUMN(5)*25, TITLE*80
Note that when declaring character arrays the string length follows
the list of array bounds. The character array COLUMN has 5
elements each of which is 25 characters long; TITLE is, of course,
just a variable 80 characters long. Although a default string length
can be set for an entire type statement, it is not possible to set a
default array size in a similar way.
It is generally good practice to use named constants to specify array bounds as this facilitates later modifications:
PARAMETER (MAXIM = 15)
INTEGER POINTS(MAXIM)
COMPLEX SERIES(2**MAXIM)
These arrays all have a lower bound of one. A different lower
bound can be specified for any dimension as shown below. The
lower and upper bounds are separated by a colon:
REAL TAX(1985:1990), PAY(12,1985:1990)
LOGICAL TRIPLE(-1:1, -1:1, -1:1, -1:1)
TAX has 6 elements from TAX(1985) to TAX(1990).Although Fortran itself sets no limits to the sizes of arrays that can be defined, the finite capacity of the hardware is likely to do so. In virtual memory operating systems it is possible to use arrays larger than physical memory: those parts of the array not in active use are held on backing store such as a disc file.
An array element reference must always use the same number of subscripts as the number of dimensions declared for the array. Each subscript can be an integer expression of any complexity, but there are restrictions on functions with side effects (see section 9.3).
An array element reference is only valid if all of the subscript expressions are defined and if each one is in the range declared for it. An array element can only be used in an expression if a value for it has been defined. A DATA statement (section 12) can be used to define an initial value for an entire array or any set of elements.
An array can be used without subscripts:
Arrays are always stored in a contiguous set of memory locations.
In the case of multi-dimensional arrays, the order of the elements
is that the first subscript varies most rapidly, then the second
subscript, and so on. For example in the following 2-dimensional
array (for simplicity one of only six elements):
The elements are stored in the following sequence:
X(1,1), X(2,1), X(1,2), X(2,2), X(1,3), X(2,3)
i.e. the sequence moves down each column first, then across to the
next row. This column order is different from that used in some
other programming languages.
The storage order may be important if you use large multi-dimensional arrays and wish to carry out some operation on all the elements of the array. It is then likely to be faster to access the array in storage order, i.e. by columns rather than rows. This means arranging loop indices with the last subscript indexed by the outer loop, and so on inwards. For example:
DOUBLE PRECISION ARRAY(100,100), SUM
SUM = 0.0D0
DO 250,L = 1,100
DO 150,K = 1,100
SUM = SUM + ARRAY(K,L)
150 CONTINUE
250 CONTINUE
With the loops arranged this way around the memory locations are
accessed in consecutive order, which minimises the processor
overhead in subscript calculations.